The previous lessons established that with the topic of Basics of Counting with Combinatorics we are able to calculate the number of possibilities in which an event can occur. I realized that we can now apply this with Probability Theory to solve much more complex probability problems. But first, we must define probability as the number of times an event can occur over the number of trials.

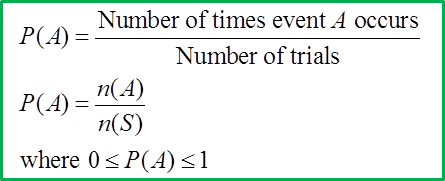
 You can really appreciate how these concepts interrelate to solve problems that are often difficult to solve without the other. An example is the problem below.

 To solve this problem, we must generate all the permutations of {1, 2, 3} in which there are 3! = 6.

These are:

 Among them, only the following show that 1 precedes 3:

 Therefore, the probability of 1 preceding 3 is 3/6 or 0.5.

 Below are other probability theorems that I also found useful in probability problems and more advanced topics such as Bayes Theorem.

Another concept that has fascinated me in this lecture was the Bernoulli trial which is the performance of an experiment with two possible outcomes such as a series of bits. The formula for finding the probability of exactly k successes in n independent Bernoulli trial with a probability of success p and probability of failure q is expressed as:

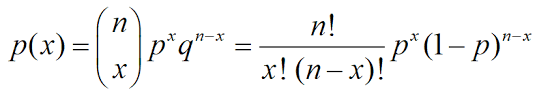
I find this to be incredibly useful in assessing the probability of guessing the value of random tasks like a coin flip. I also have encountered numerous problems that have been modeled from this principle such as the life and death distribution of a department of a hospital and many others.

The world of probability is vast and filled with sophisticated principles which dictate all events in the universe. With the proper knowledge of these principles, we can predict and manipulate the choice of the dice who play god.