The starting lessons of Discrete Mathematical Structures in Computer Science II were certainly not what I have expected. At first, I thought we would dive deeper into the previous semester’s topic on linear algebra and its applications in computer science. I was surprised when we started off with a much easier topic of Basic Counting Principles. Little did I know that this lesson would be the foundation of what was yet to come.

 The main principles introduced in this lesson were the Product Rule and the Sum Rule. The product rule or multiplication principle states that if there are a ways of doing something and b ways of doing another thing, then there are a · b ways of performing both actions.

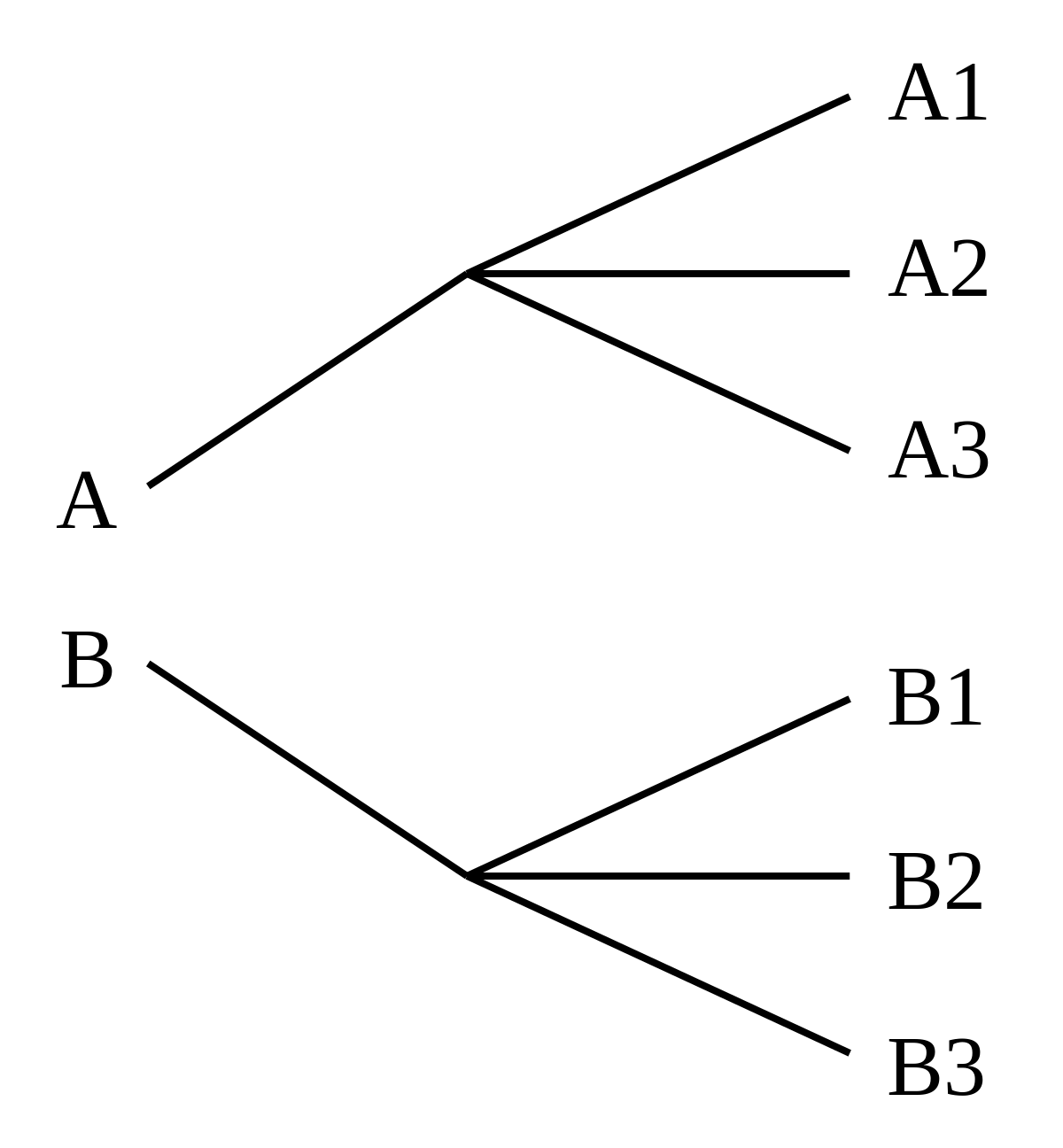
 The Sum rule, on the other hand, states that if a task can be done either in one of a ways or in one of b ways, where none of the set of a ways is the same as any of the set of b ways, then there are a+b ways to do the task.

 These principles can be applied in almost any field of mathematics but in the course, it is often used in combinations and permutations. I was fascinated by how such a simple principle could be applied in so many industries. One common problem that intrigued me was the one below:

 Since repeating is allowed, the number of strings of 5 lowercase alphabet letters is 26⁵. To get the string with an x in them we must subtract this with the number of strings without an x which is 25⁵. Therefore, the answer is 26⁵-25⁵ which is equal to 2,115,751.

 As we seen above, the answers to these questions come by the millions. Assuming that this was a password for an online system it's amazing how unlikely a user can just guess a password considering how large the result is. It's much more mind-blowing if you realize that we know this fact by using the simple rules we learned above.