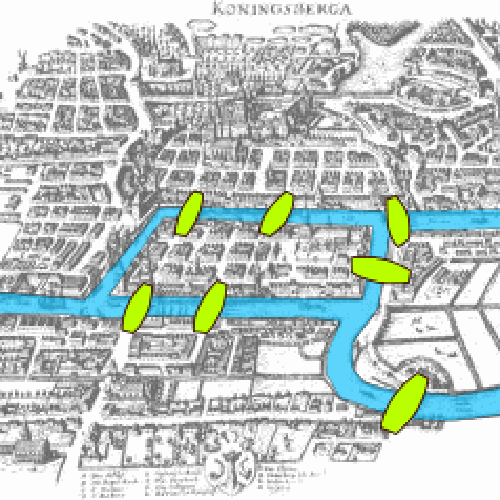
Who knew that one of the most famous and utilized fields in mathematics originated from the thoughts of a curious Prussian Mayor. Carl Gottlieb Ehler found himself at his wit's end when he contacted Leonhard Euler to ask about a simple thought experiment about a set of bridges in the City of Königsberg. The problem that boggled his mind is stated as follows:

 Euler grappled with the idea and later invented a new kind of geometry that would be the backbone of solving these kinds of problems. Thus, it marked the beginning of the field of Graph Theory. Naturally, Euler would name such a grand discovery to himself, hence we have the Eulerian Path. The Eulerian path describes a path in a graph that uses each edge precisely once. If such a path exists, the graph is called traversable. An Eulerian circuit, on the other hand, describes a cycle that uses each edge precisely once. If such a cycle exists, the graph is called Eulerian.

 We can identify Eulerian Paths and Circuits with the following theorems.

 We can represent the Königsberg problem with the graph below.

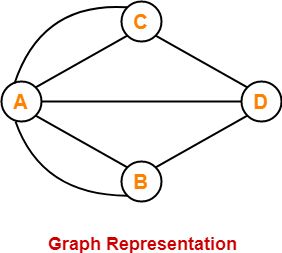
 Since our graph has exactly four vertices of odd degrees, it is not an Eulerian Path. Therefore, it is impossible for someone to cross all 7 bridges without crossing any of them more than once.

 There is also a Hamiltonian Path that deals with a different class of problems which focuses on graphs that visit each vertex exactly once. In this case, Königsberg has a Hamiltonian Path.

 It is simply amazing how such random and seemingly trivial questions can transform into theorems that become the foundations of modern technology. It is so fascinating to discover how these stories of invention unfold and to witness their applications centuries after. I also find it comical how Carl Gottlieb Ehler and Leonhard Euler's question about bridges led to Google, a system that can answer almost any question.