For me, the topic of Algebraic Structure and Groups has been the newest and most challenging concept I have ever encountered in the course. I simply have never encountered something like it.

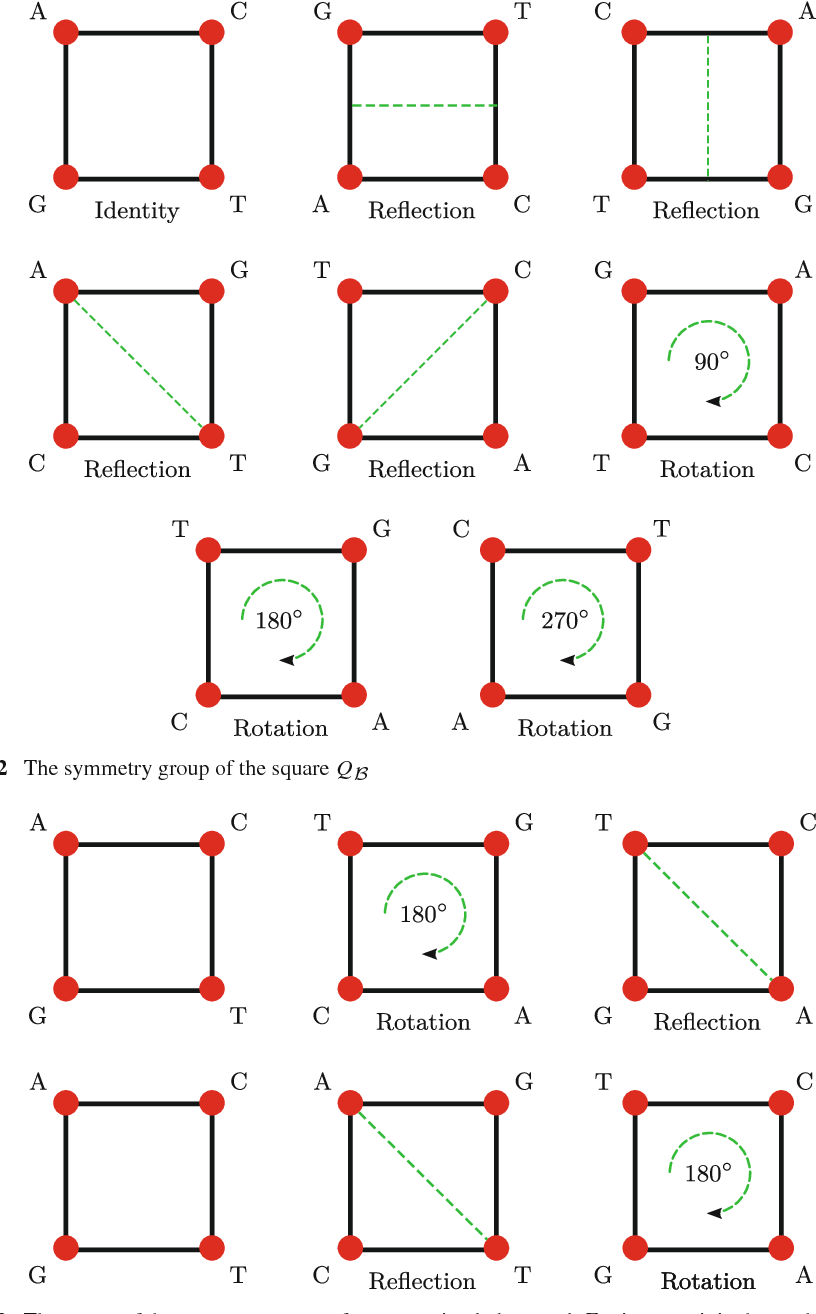
 At first, the introduction with symmetries of the square and its segway toward binary operations was very unintuitive for me. It was only when I learned the topic of groups that I found their connection. To review, a group is a set S and a binary operation such that:

1. is associative for all elements in S
2. There exists an identity element e for all elements in S
3. There exists an inverse element e for all elements in S

 Knowing this, I was amazed to see how this can be used to model geometric patterns such as the symmetries of the square problem we have encountered previously. Later on, I learned more examples of groups through the materials with modular/clock arithmetic as its prime example.

 I also had a wonderful time implementing the Euclidean Algorithms in Python to find the modular multiplicative inverse and GCD. Implementing the algorithm certainly made the lab exercises much easier. It probably took me days before really grasping the distinction between Groups, Rings, and Fields but in the end, it was really rewarding. I really look forward to seeing what else is in store for this topic as I move forward in my journey in computer science.